How to Analyze Time And Space Complexity of Algorithms

Hey, Tea Lovers! Starting your data structures and algorithm journey? Trying to solve more LeetCode or HackerRank or want to win Google CodeJam? Then this is the first thing you should know about, Time and Space Complexity of an Algorithm. We will see various ways we figure out the complexity, and how it is useful to determine the efficiency of an algorithm. With this, we can easily find out the Optimal Solution or algorithm among multiple.

This will be our first in the series of Data Structures and Algorithms on CodersTea. I will create an index page listing all these topics in order from basic to advance. If you don’t want to miss that out, you can subscribe to our website or follow us on social media.

I would be happy to connect with you guys on social media. It’s @coderstea on Twitter, Linkedin, Facebook, Instagram, and YouTube.

Please Subscribe to the newsletter to know about the latest posts from CodersTea.

In Computer Science, Computational Complexity explains algorithm performance. This topic itself is vast and in-depth, but we try to keep it as simple as possible so that you can easily learn and crack the #FAANG interviews. In the next few paragraphs, we will discuss Time and Space Complexity + Big 0 Notation.

I can understand you’re in a hurry to prepare for the interview, so let’s quickly hum right into it. But before, prepare your cup of tea to sip and code with me.

Computational Complexity

• Computational Complexity or Simply Complexity is a computer science concept that focuses on the number of computing resources required to run a task.
• Algorithmic Complexity is a way of comparing the efficiency of an algorithm. It is possible to measure Complexity in terms of how long it takes for a program to run (time complexity) or how much memory it will consume (space complexity).

The complexity of an Algorithm

The complexity of an Algorithm is done on a comparative scale. Following are the different types and best to worst. Also, in the end, we have a graph showing how they compare with each other.

Constant Complexity – O(1)

• It imposes a complexity of O(1).
• It undergoes an execution of a constant number of steps like 1, 2, and 3. for solving a given problem.
• The count of operations is independent of the input data size.

for example,

int n = 10;
System.out.println("value of n is : " + n);Code language: JavaScript (javascript)

In the above example, It’s not dependent on the value of n & always takes a constant/same amount of time to run.

Logarithmic Complexity – O(log n)

• It imposes a complexity of O(log(N)).
• It undergoes the execution of the order of log(N) steps. To perform operations on N elements, it often takes the logarithmic base as 2.
• Constant time algorithms are (asymptotically) the quickest. Logarithmic time is the next fastest. Unfortunately, It is harder to imagine.
• One well-known example of a logarithmic time algorithm is the binary search algorithm.

for example,

for (int i = 1; i < n; i = i * 2){
    System.out.println("value of i is : " + i);
}Code language: HTML, XML (xml)

If n is 4, the output will be the following:

value of i is : 1
value of i is : 2

In the above example complexity is log(4) = 2.

Linear Complexity – O(n)

• It imposes a complexity of O(N).
• If we say something grows linearly, we mean that it grows directly proportional to the size of its inputs.
• It encompasses the same number of steps as the total number of elements to implement an operation on N elements.

for example,

for (int i = 0; i < n; i++) {
    System.out.println("value of i is : " + i);
}Code language: JavaScript (javascript)

If n is 4, the output will be the following:

value of i is : 0
value of i is : 1
value of i is : 2
value of i is : 3

In the above example complexity is O(4) = 4.

It’s dependent on the value of n, & it always runs the loop for the n value.

N Log N Complexity – O(n log n)

• It imposes a complexity of O(n log n).
• It is the somehow combination of Linear + Logarithmic complexity.
• The running time grows in proportion to the n log n of the input.

for example,

for (int i = 1; i <= n; i++){
    for(int j = 1; j < n; j = j * 2) {
        System.out.println("value of  i : " + i + " and j : " + j);
    }
}Code language: JavaScript (javascript)

If n is 4, the output will be the following:

value of  i : 1 and j : 1
value of  i : 1 and j : 2
value of  i : 2 and j : 1
value of  i : 2 and j : 2
value of  i : 3 and j : 1
value of  i : 3 and j : 2
value of  i : 4 and j : 1
value of  i : 4 and j : 2

In the above example, complexity is
O(4) = 4 * log(4) = 4 * 2 = 8.

Polynomial Complexity – O(n^p)

• It imposes a complexity of O(n^p).
• The term polynomial is a general term that contains quadratic (n2), cubic (n3), and quartic (n4) functions.

Quadratic Complexity – O(n²)

• It imposes a complexity of O(n²).
• For N input data size, it undergoes the order of N2 count of operations on N number of elements for solving a given problem.

Cubic Complexity – O(n³)

• It imposes a complexity of O(n³).
• For N input data size, it undergoes the order of N3 count of operations on N number of elements for solving a given problem.

& so on…

for example,

for (int i = 1; i <= n; i++) {
    for(int j = 1; j <= n; j++) {
        System.out.println("value of  i : " + i + " and j : " + j);
    }
}Code language: JavaScript (javascript)

If n is 4, the output will be the following:

value of  i : 1 and j : 1
value of  i : 1 and j : 2
value of  i : 1 and j : 3
value of  i : 1 and j : 4
value of  i : 2 and j : 1
value of  i : 2 and j : 2
value of  i : 2 and j : 3
value of  i : 2 and j : 4
value of  i : 3 and j : 1
value of  i : 3 and j : 2
value of  i : 3 and j : 3
value of  i : 3 and j : 4
value of  i : 4 and j : 1
value of  i : 4 and j : 2
value of  i : 4 and j : 3
value of  i : 4 and j : 4

This algorithm will run 4² = 16 times. Note, if we were to nest another for loop, this would become an O(n²) algorithm.
In the above example, complexity is O(n²) = 16.

Exponential Complexity – O(kⁿ)

• It imposes a complexity of O(kⁿ).
• These grow in proportion to some factor exponentiated by the input.
• For N elements, it will execute the order of the count of operations that is exponentially dependable on the input data size.

for example, Let’s have a look at a simple example of an O(2ⁿ) Time Algorithm:

for (int i = 1; i <= Math.pow(2, n); i++){
    System.out.println("value of i is : " + i);
}Code language: JavaScript (javascript)

If the n is 4, thus this example will run 2⁴ = 16 times.

Factorial Complexity – O(n!)

• It imposes a complexity of O(n!).
• To solve the traveling salesman problem using a brute-force approach.
• This class of algorithms has a run time proportional to the factorial of the input size.

for example, Let’s have a look at a simple example of an O(n!) time algorithm:

for (int i = 1; i <= factorial(n); i++){
    System.out.println("value of i is : " + i);
}Code language: JavaScript (javascript)

If n is 4, thus this algorithm will run 4! = 24 times.

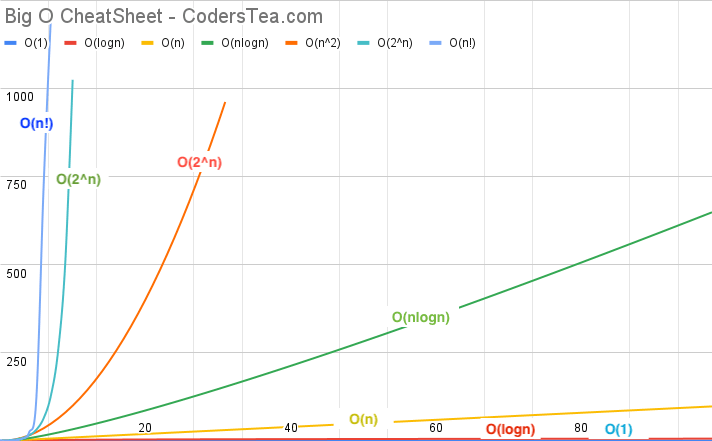
Complexity Comparision

Following is the graph of mentioned time complexities. The X-Axis is the number of elements, and Y-Axis is how much time it will take in various complexity. As you can see O(1) and O(logN) are hardly changed, but 2^n and n! are like piercing the sky.

Types of Analysis For Complexity

Worst-case time complexity

• Worst-case time complexity defines as the maximum amount of time required to complete its execution.
• Thus, it is nothing but a function defined by the maximum number of steps performed on an instance.

Average-case time complexity

• Average-case time complexity defines as the average amount of time required to complete its execution.
• Thus, it is nothing but a function defined by the average number of steps performed on an instance.

Best-case time complexity

• Best-case time complexity defines as the minimum amount of time required to complete its execution.
• Thus, it is nothing but a function defined by the minimum number of steps performed on an instance.

What is Asymptotic in Computation Complexity

Asymptotic curves and lines are those that get closer but do not intersect.

Asymptotic analysis

• It is a technique for representing limiting behavior. The methodology has applications across science. It is for analyzing the performance of algorithms on large data sets.
• In computer science, the analysis of algorithms, considering the performance of algorithms when applied to large input datasets

for example,

function <em>ƒ (n) = 4n<sup>2</sup>+5n</em>Code language: HTML, XML (xml)

1. The term 5n becomes insignificant compared to 4n²
2. and In 4n², 4 becomes insignificant compared to n²
3. When n is large. The function “ƒ (n) is said to be asymptotically equivalent to n² as n → ∞“,
4. and here is written symbolically as ƒ (n) ~ n² or  ƒ (n) = n²

Why is Asymptotic Notation Important?

• They give easy characteristics of an algorithm’s efficiency.
• They allow comparisons of the performances of various algorithms.

Types of Asymptotic Notations

• It is used to write the fastest and slowest possible running algorithm. ‘Best-case’ and ‘worst-case’ scenarios are referred to as such.
• We derive the complexity concerning the size of the input. (Example in terms of n).
• These notations are essential because without expanding the cost of running the algorithm, we can estimate the complexity of the algorithms.
• Asymptotic Notation is a way of comparing functions that ignores constant factors and small input sizes. Three notations are used to calculate the running time complexity of an algorithm.
• Asymptotic Notation is a way of comparing functions that ignores constant factors and small input sizes. Three notations calculate the running time complexity of an algorithm.

Big O notation (pronounced “big oh”) – O (g (n))

• Big-oh is the formal method of expressing the upper bound of an algorithm’s running time.
• It is an Asymptotic Upper Bound.
• The complexity of f(n) expresses as O (g (n)).
• It is the measure of the maximum amount of time.

Omega notation – Ω (g (n))

• Omega is the formal method of expressing the lower bound of an algorithm’s running time.
• It is an Asymptotic Lower Bound.
• The complexity of f(n) expresses as Ω (g (n)).
• It is the measure of the minimum amount of time.

Theta notation – θ (g(n))

• The Theta Notation is more precise than both the big-oh and Omega notation. The function f (n) = θ (g (n)) if g(n) is both an upper and lower bound.
• It is an Asymptotic Tight Bound.
• The complexity of f(n) express as θ (g(n)).
• It is the measure of the exact amount of time.

Types of Complexity ( Based on Resources )

Based on the resource, we can divide them into two types,

1. Time Complexity
2. Space Complexity

We will Focus on Time & Space Complexity. There are more types of complexity that we will discuss in short.

Time Complexity

• It is measured as the amount of time that an algorithm needs to run.
• Computational time complexity describes the change in the runtime of an algorithm, depending on the change in input data’s size.
• In other words, How much an algorithm degrades as the amount of input data (n) increases.

for example,

We will be measuring Time complexity with the worst-case scenario.
In linear search, We need to check each index until we get the desired result. Let’s assume the below is that array.
Given the array:

• If you search for a 5, you only need to perform one comparison as it’s in the zero indexes.
• If you search for a 9, you need to perform four comparisons as it’s in the fourth index. 
• If you search for a 4, you need to perform six comparisons as you will check each box in turn and not find it in any of them.

In the above example, When you search for a number that isn’t present in an array. In this case, we must check the entire array, Therefore, this is an example of a worst-case scenario.

In the worst case, the time taken for a linear search is directly dependent on the size of the input, so as the size of the arrays grows, the required time also grows respectively.

The worst-case scenario provides a good benchmark for an algorithm to compare its time complexity for solving the problem.

Space Complexity

• It is measured the amount of memory that an algorithm needs to run.
• Space complexity includes both Auxiliary space and space used by input.
• Describes how much additional memory an algorithm needs depending on the size of the input data.

Auxiliary Space is the extra space or temporary space used by an algorithm. 

• If we create a two-dimensional array of size n*n, we will need O(n²) space.
• Space complexity is a parallel concept to time complexity. If we need to create an array of size n, this will require O(n) space. If we create a two-dimensional array of size n*n, we will need O(n²) space.
• The stack space also counts in recursive calls. 

for example,

int total = 0;
int n = 5;

for (int i = 1; i <= n; i++){
    total += i;
}

System.out.println("n value is : " + n);
System.out.println("total value is : " + total);Code language: JavaScript (javascript)

In the above example, the value of a total variable is stored sum over & over again, hence the space complexity is constant.

Some Other Types of Complexity

Arithmetic Complexity

• Binary Representation is an upper bound size of the number that occurs during a computation.
• The time complexity is generally the product of the arithmetic complexity by a constant factor.

Bit Complexity

• Bit Complexity refers to the number of operations on bits, required for running an algorithm.
• With most models of computation, it equals the time complexity up to a constant factor.
• On Computers, the number of machine word operations required is proportional to the bit complexity.
• So, the time complexity and the bit complexity are equivalent to realistic models of the computation

Big O notation – O (g (n))

The big O notation uses for the expression of an algorithm’s complexity regarding the growth of the input size. Hence, it ranks algorithms based on their performance with large inputs.

What is Big O notation?

• Knowing the time and space needed to solve a problem allows different algorithms to compare.
• A key aspect that affects both types of complexity is the size of the input that is fed into the algorithm.
• Time complexity indicates the time an algorithm takes to run & Space complexity refers to the amount of memory required by an algorithm to solve a problem.
• How an algorithm’s time and space complexity changes (increases, decreases, or remains stable) when the size of the input changes is known as the ‘order of growth’ of the algorithm.

Key points about Big O Notation:

Here are some highlights of Big O Notation:

• Big O is concerned with large inputs.
• Big O notation is a framework to analyze and compare algorithms.
• Big O notation cares about the worst-case scenario for that algorithm.
• Big O needs to lower the time complexity function to have better performance.
• Amount of work CPU has to do (time complexity) as the input size grows (towards infinity).
• Big O = Big Order function. Drop constants and lower-order terms. E.g. O( 4n² + 5n + 3 ) becomes O(n2).
• Calculate the time complexity of an algorithm or program, The most common metric it’s using Big O notation.

Complexity will usually vary with the size of the input When we have a choice from several different approaches to solving a problem. Big O notation allows us to readily compare one algorithm to another To help us choose the best option.

For instance, if you have a function that takes an array as an input, if you increase the number of elements in the collection, you still perform the same operations; you have a constant runtime. On the other hand, if the CPU’s work grows proportionally to the input array size, you have a linear runtime O(n).

Calculating Big O time complexity

• To find the Big O of an algorithm, you need to focus on the growth of its most significant part.
• It depends on the large input values of the complexity of the problem, & that large value is dominant over the other part & the remaining small value & their effect are insignificant.

Let’s understand this example,

for example,

In Linear Search is an algorithm time complexity of f(n) = 2n + 3

in f(n) = 2n + 3

To Solve this divide it into two parts as

1. 2n
2. 3

In the first part, have 2n, which loop of repeats a maximum n time, so consider large value as n, so consider n value,

& in the second part, we have a constant value of 3, which is insignificant as compared to the order of n, & so you can ignore the constant value.

Big O notation cares about the worst-case scenario.

Linear Search is an algorithm, Big O described as, O(n).

Time & Space Complexity of Java Collection Framework

Conclusion

We talked about computational complexity & Explored it in detail about them. For beginners, it might be a lot to digest but trust me, It will get cleared once you start working. Just don’t lose hope to gain your knowledge not by reading only but by working on some stuff side by side.

I have posted some posts that will help you, such as “Mistakes Probably Every Programmer and I Made in the Beginning”, “Most Loved Interview Question: How HashMap works in Java” & “interview series”

Hope you liked the post. If you want to discuss something and clear out some questions related or unrelated to this topic, please free to comment. or Follow us on social media. See you in the next post.

See you in the next post. HAKUNA MATATA!!!

I would be happy to connect with you guys on social media. It’s @coderstea on Twitter, Linkedin, Facebook, Instagram, and YouTube.

Please Subscribe to the newsletter to know about the latest posts from CodersTea.